
Ex 5 3 9 Find Dy Dx In Y Sin 1 2x 1 2x2 Chapter 5
If (x2 y2)2 = xy, find dy/dx Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesLet's simplify it First dy/dx = (y/x 1)/(y/x 1) Taking y = vx dy/dx = v xdv/dx Therefore, dx/x = (v 1)dv / (v^2 1) Integrating we get log (1/x) logc = arctan (y/x) 1/2 log
If y=sec^(-1)((x^(2)+1)/(x^(2)-1)) find (dy)/(dx)
If y=sec^(-1)((x^(2)+1)/(x^(2)-1)) find (dy)/(dx)-This problem has been solved!After solving d^2y/dx^2 my answer was 1/ (4t^3), not sure what to do after
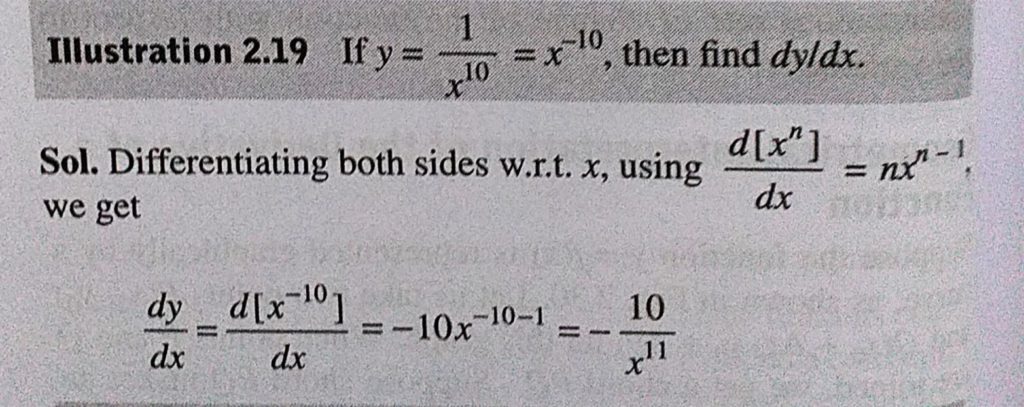
If Y 1 X 10 X 10 Then Find Dy Dx Sahay Sir
See the answer find dy/dx and d^2y/dx^2 x=t^21 y=t^2t For which values of t is the curve concave upward?Y=2x^21 differentiate wrt x dy/dx=d/dx (2x^21) dy/dx=2 (2x)0 dy/dx=4x by use of chain rule dy/dx= (dy/dt) (dt/dx) put dy/dx=4x and dy/dt=1 4x= (1)dt/dxExplanation This is a nonhomogeneous linear differential equation After multiplying by x2 we get x2y′ (x2 −1)y = x3 x2 − x Step 1 Let y(x) = w(x)1 Then y′(x) = −w(x)21 ⋅w′(x), so the differential equation becomes w(x)2(1x)2w′(x)xw(x)x2 = 0, that is w′(x) (1x)2x w(x) (1x)2x2 = 0 Let t = xy
dy/dx=x/y x^2y^2=1 Differentiate wrt x d/dxx^2d/dxy^2=d/dx1 We already know how to deal with the first and third terms, so lets get them out the way d/dxx^2d/dxy^2=d/dx1 2xd/dxy^2=0 For the remaining term we use the chain rule, we don't know how to differentiate y^2 wrt x but we do know how to differentiate y^2 wrt y (it the same as differentiating x^2 wrt x!)Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepCalculus Find dy/dx y^2=1/ (1x^2) y2 = 1 1 − x2 y 2 = 1 1 x 2 Differentiate both sides of the equation d dx (y2) = d dx ( 1 1−x2) d d x ( y 2) = d d x ( 1 1 x 2) Differentiate the left side of the equation Tap for more steps 2yy' 2 y y ′ Differentiate the right side of the equation
If y=sec^(-1)((x^(2)+1)/(x^(2)-1)) find (dy)/(dx)のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 4 2 Implicit Differentiation | 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
4 2 Implicit Differentiation |  4 2 Implicit Differentiation | 4 2 Implicit Differentiation |
4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation | 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
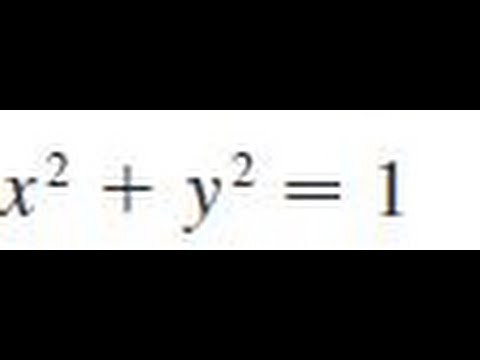 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation | 4 2 Implicit Differentiation | 4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation | 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation | 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation | 4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
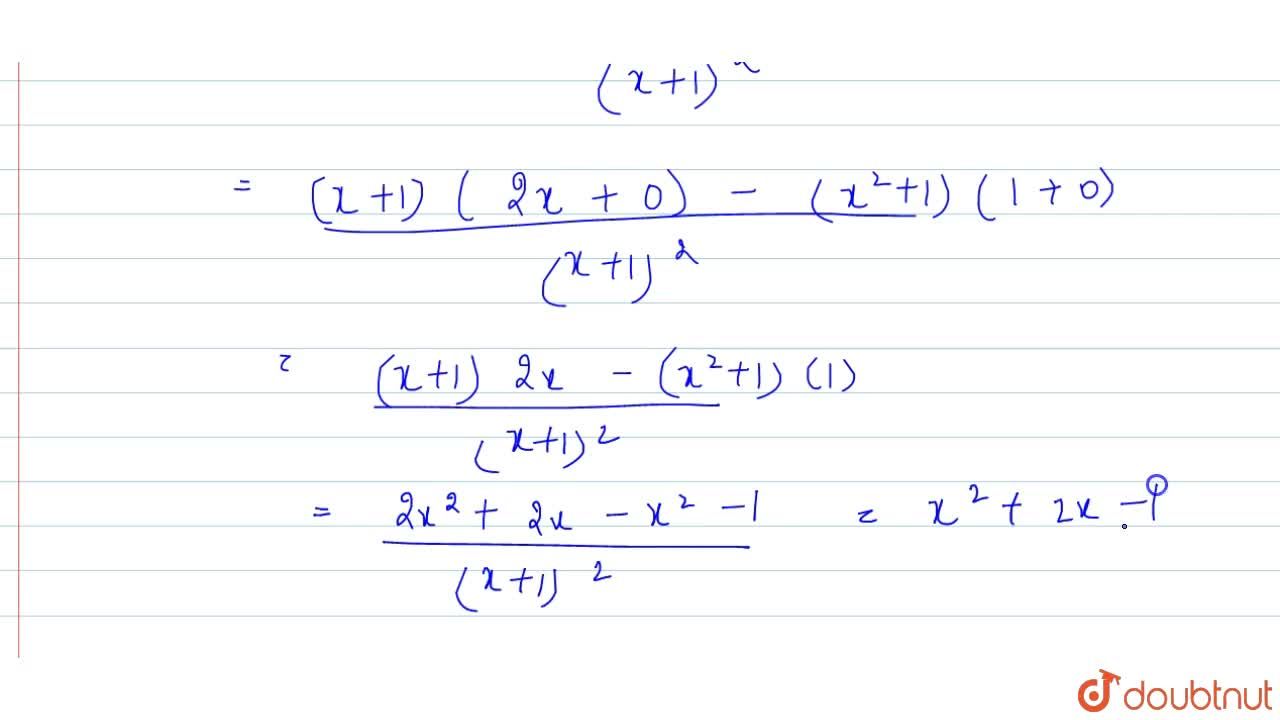 4 2 Implicit Differentiation | 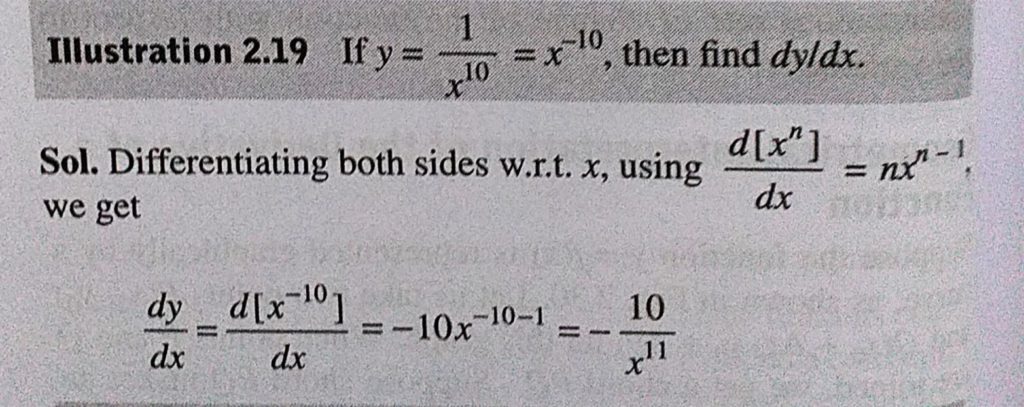 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
4 2 Implicit Differentiation | 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
4 2 Implicit Differentiation | 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation | 4 2 Implicit Differentiation | 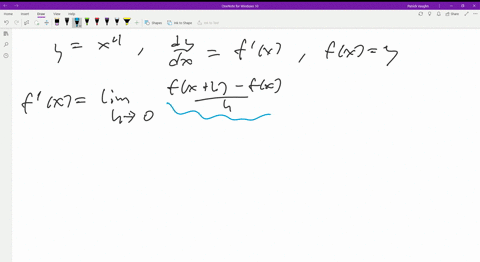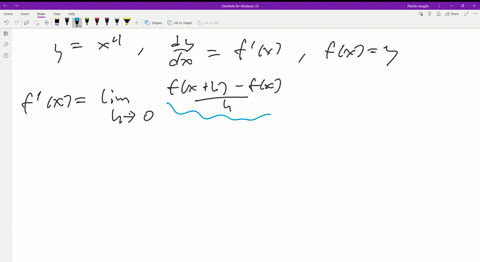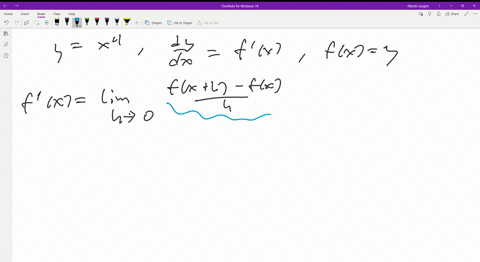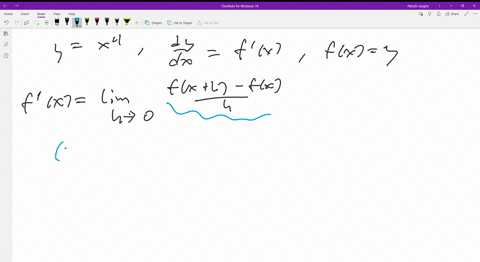 4 2 Implicit Differentiation |
 4 2 Implicit Differentiation | 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
4 2 Implicit Differentiation | 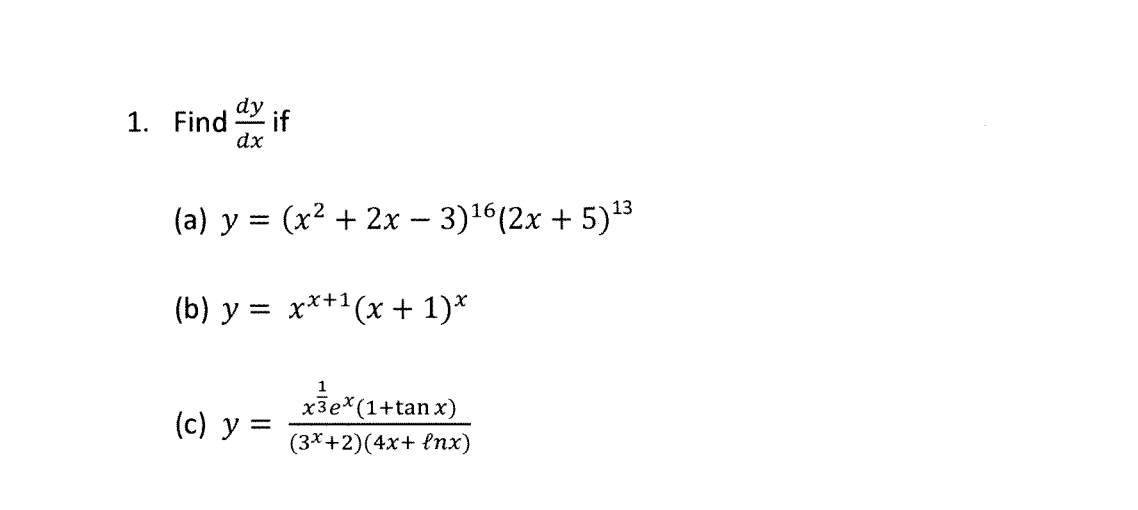 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation | 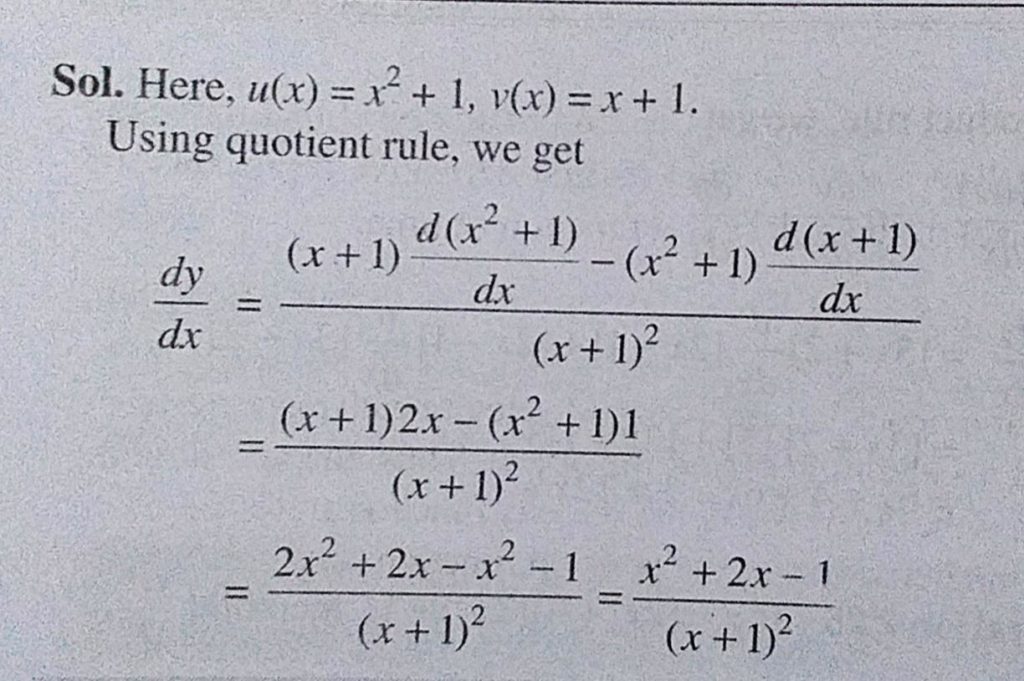 4 2 Implicit Differentiation |
 4 2 Implicit Differentiation | 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation | 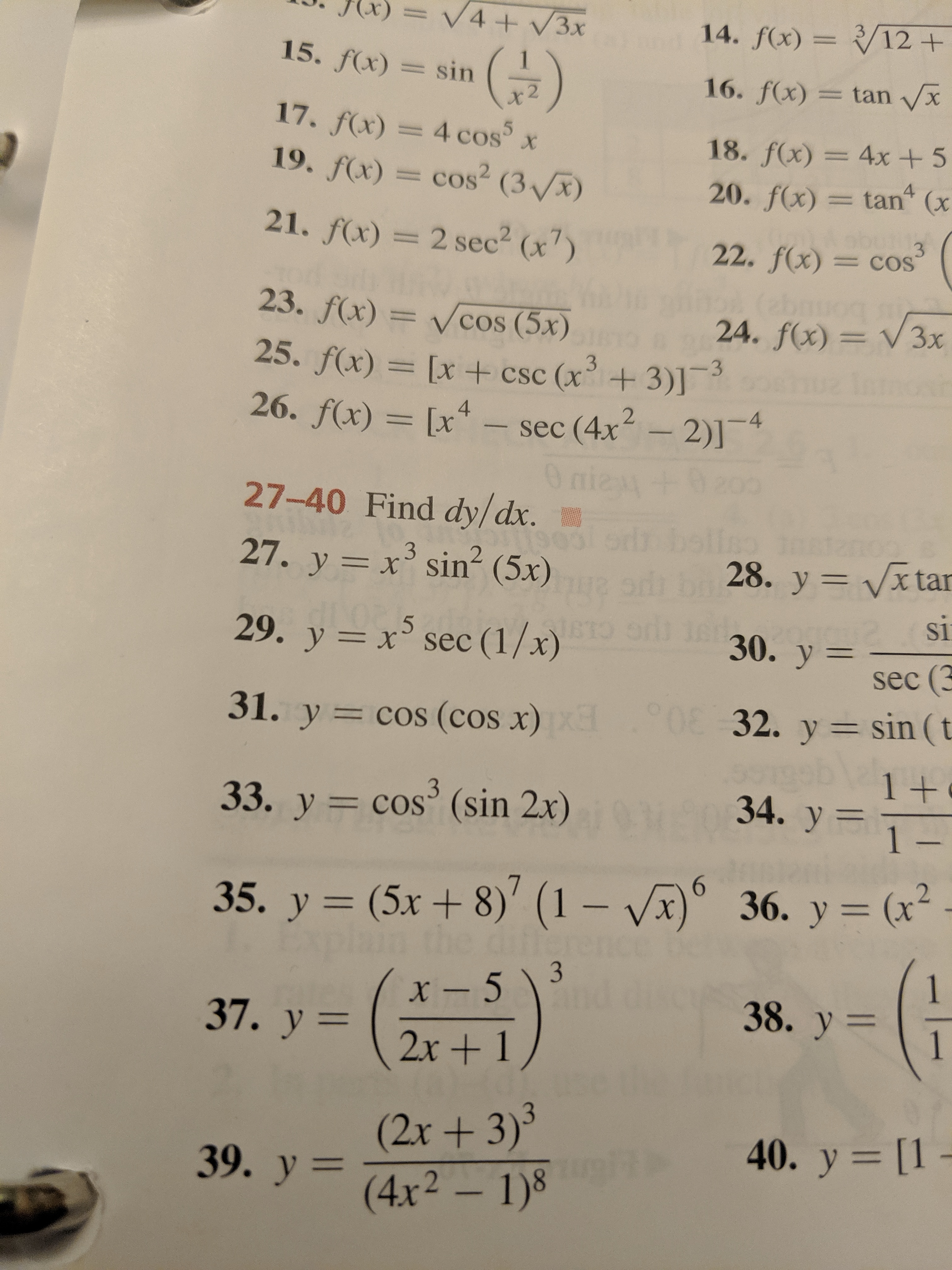 4 2 Implicit Differentiation |
4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
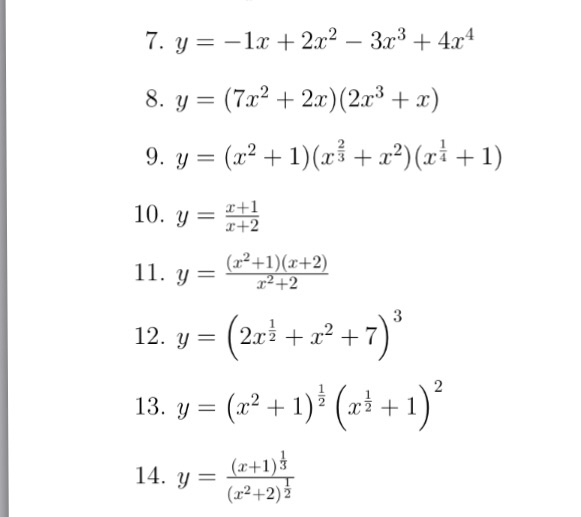 4 2 Implicit Differentiation | 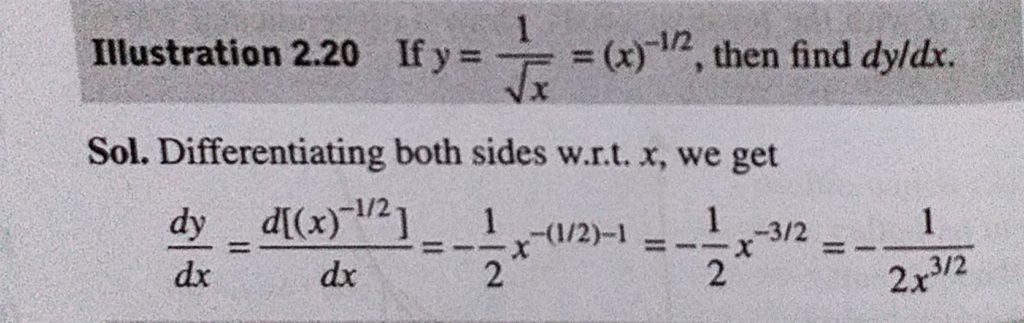 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation | 4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
 4 2 Implicit Differentiation |  4 2 Implicit Differentiation |
Find \frac{dy}{dx} \\ y=(1x^2)^{\arctan(\sinh x)} Use first principles to find the derivatives of the following functions Confirm the solution by using the derivative shortcuts General Motors (GM) wants to swap out of $15,000,000 of fixed interest rate debt and into floating interest rate debt for 3 years Suppose the fixed interest rate is dy/dx=\sqrt{y/x} Given that x^{1/2}y^{1/2}=a^{1/2} differentiating above equation wrt x on both sides as follows d/dx(x^{1/2}y^{1/2})=d/dx(a^{1/2}) 1/2x^{1/21}1/2y^{1/21}dy/dx=0 x^{1/2}y^{1/2}dy/dx=0 1/{\sqrtx}1/{\sqrty}dy/dx=0 1/{\sqrty}dy/dx=1/\sqrtx dy/dx=\sqrt{y/x}
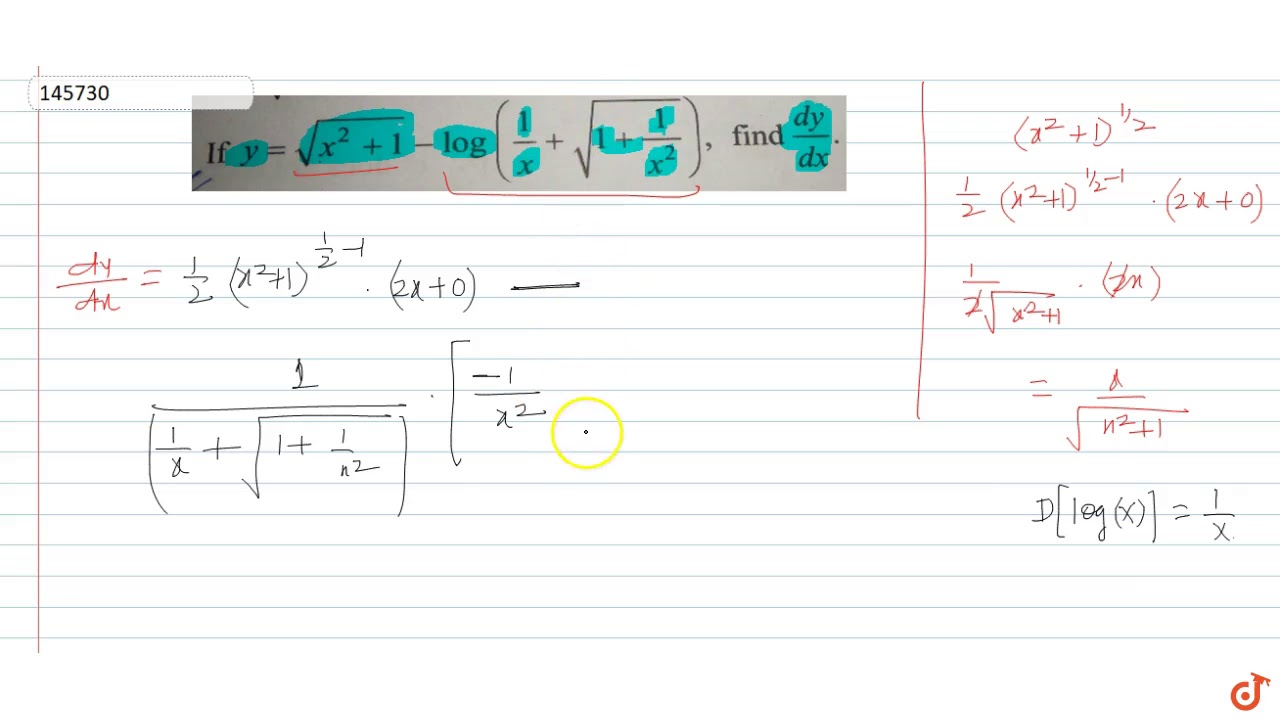
Incoming Term: y=x^2+1/x^2 find dy/dx, y=log(1-x^2/1+x^2) find dy/dx, y=tan^-1(1-x^2/1+x^2) find dy/dx, y=sin^-1(1-x^2/1+x^2) find dy/dx, y=cos^-1(1-x^2/1+x^2) find dy/dx, if y=(1-x^2/1+x^2) find dy/dx, y=(x-1)(x-2)/√x find dy/dx, let y = (x - 1)(x + 2). find dy/dx, y=ln(x^2+1)/x find dy/dx, if y=sec^(-1)((x^(2)+1)/(x^(2)-1)) find (dy)/(dx),




0 件のコメント:
コメントを投稿